Ранее мы приводили формулы, позволяющие определить интервал неопределенности расчетных потерь электроэнергии при заданных погрешностях исходных данных о нагрузках. Задача определения мощности КУ, обеспечивающих гарантированный экономический эффект, может решаться в двух постановках:
1) определение интервалов неопределенности экономического эффекта от установки КУ, мощность которых определена на основе расчетных нагрузок;
2) определение интервалов неопределенности мощности КУ в каждом узле.
В первом случае используют непосредственно формулы для интервалов неопределенности потерь электроэнергии, во втором — формулы для интервалов неопределенности производных, на основе которых рассчитывают мощности КУ.
Формулы, приведенные в прил. 4, выведены для двух вариантов расчета: при известной суммарной нагрузке сети (ситуация, характерная для условий эксплуатации) и при отсутствии таких данных (проектная задача). Выбор КУ следует отнести к проектным задачам. Кроме того, если суммарная активная нагрузка сети является показателем, определяющим сумму узловых нагрузок, то суммарная реактивная нагрузка теряет эти свойства в связи с ее искажением генерацией и большими потерями реактивной мощности в линиях, а также работой других источников реактивной мощности. Поэтому в данной задаче приходится применять формулы для несбалансированных нагрузок.
Расчет интервалов неопределенности экономического эффекта от установки КУ
Абсолютные погрешности узловых нагрузок являются исходными данными и остаются постоянными в процессе расчета, а относительные погрешности изменяются в связи с уменьшением нагрузок. Результаты расчета будут одинаковыми при использовании как тех, так и других погрешностей, но для того, чтобы не вычислять относительные погрешности при конечных нагрузках, воспользуемся формулой (П4.20) для абсолютных погрешностей. Применительно к реактивным нагрузкам она имеет вид:
Погрешность, вносимая в расчет потерь в сети погрешностью реактивной нагрузки i-го узла, определяется по формуле:
где qu= 2/U² (для условий примера 2/220² = 0,41 • 10-4). Рассчитаем Δyi и ΔyΣ для условий примера при одинаковой относительной погрешности узловых реактивных нагрузок, равной 10 %, что соответствует абсолютным погрешностям 3, 4 и 6 Мвар, соответственно. При этом интервалы неопределенности нагрузок узлов составляют (30 ± 3) Мвар; (40 ± 4) Мвар и (60 ± 6) Мвар. Значения ci при начальных и конечных нагрузках узлов приведены в предыдущем расчете.
Значения Δy, максимальных δРмакс и минимальных δРмин вкладов узлов в потери мощности в сети при начальных и конечных нагрузках узлов составляют, МВт: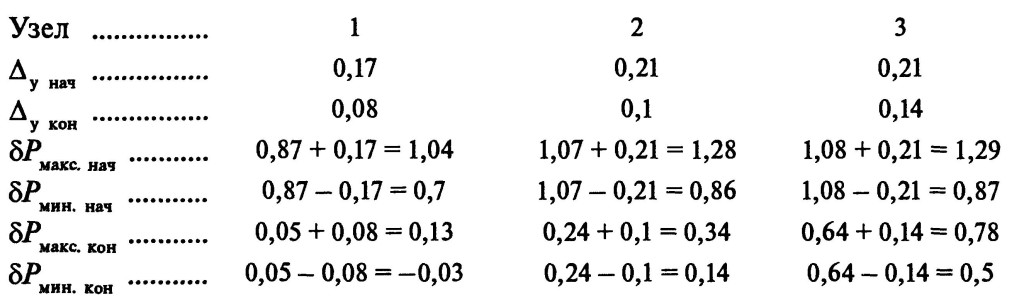
Отрицательная нижняя граница расчетного вклада первого узла в потери мощности в сети при конечных нагрузках узлов физически необъяснима, так как минимальная нагрузка узла остается положительной: 3,6 — 3 = 0,6 Мвар. Если бы она перешла через ноль и стала генерацией, то ее воздействие, очевидно, снижало бы общие потери. В данном же случае проявляется описанная в прил. 4 неточность формул, обусловленная линеаризацией функции потерь и приводящая к некоторому завышению отрицательной и занижению положительной погрешности в величине потерь. Эта неточность проявляется при больших погрешностях нагрузок, а погрешность нагрузки первого узла, равная 3 Мвар, по отношению к конечному значению нагрузки 3,6 Мвар составляет 83 %. Поэтому эффект перехода расчетного вклада в потери через нулевое значение проявился раньше, при небольшом положительном значении нагрузки. При использовании более точных формул интервал вклада, скорее всего, передвинулся бы вверх на 0,04 МВт и составил бы от 0,01 до 0,17 МВт. Тем не менее рассчитаем интервалы неопределенности экономического эффекта от установки КУ в каждом узле при тех значениях вкладов, которые получились по данным формулам.
Суммарная погрешность ΔyΣ , определяемая по формуле (7.25), при начальных нагрузках составляет 0,34 МВт, при конечных нагрузках — 0,19 МВт. Максимальные и минимальные значения потерь мощности при начальных и конечных нагрузках составят: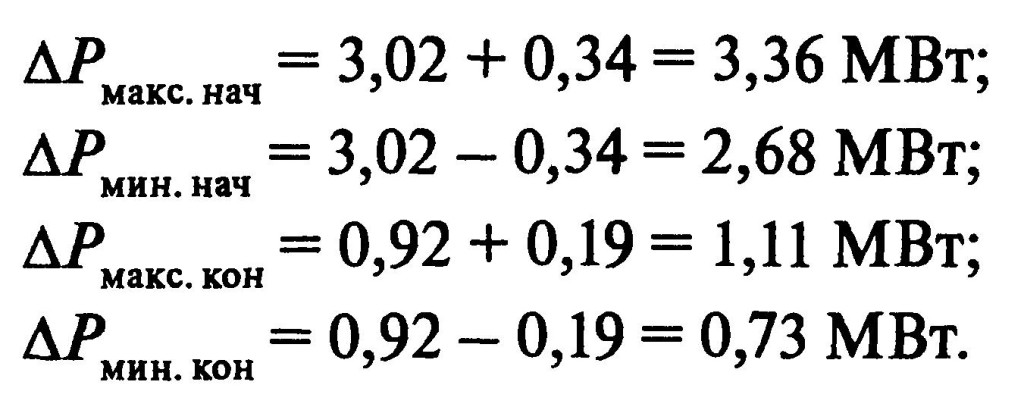
Максимальные и минимальные границы интервалов неопределенности снижения потерь δΔРмакс и δΔРмин, снижения затрат на потери δЗп.макс и δЗп.мин , снижения суммарных затрат на потери и на КУ δЗп.макс и δЗмин и срока окупаемости капиталовложений Ток.макс и Ток.мин составляют:
С помощью аналогичных расчетов определим интервалы неопределенности индивидуальных экономических показателей КУ в каждом узле.
Интервал вклада первого узла в потери мощности в сети при начальных нагрузках составляет от 0,87 — 0,17 = 0,7 МВт до 0,87 + 0,17 = = 1,04 МВт, а при конечных нагрузках от 0,05 — 0,08 = -0,03 МВт до 0,05 + 0,08 = 0,13 МВт.
Минимальное снижение потерь от установки КУ в первом узле составляет δΔРмин = 0,7 — (-0,03) = 0,73 МВт, максимальное δΔРмакс = 1,04 — 0,13 = 0,91 МВт. Снижение затрат на потери составит от δЗп.мин = 0,73 • 8 • 10-³ = 5,8 до δЗп.макс = 0,91 • 8 • 10-³ = 7,28 млн руб. в год. Стоимость КУ в первом узле Кку = 26,4 • 0,8 = 21,12 млн руб., а ежегодные затраты на их обслуживание Зо = ро Кку/100 = 5 • 21,12 / 100 = 1,06 млн руб. Интервал снижения суммарных затрат на потери и на КУ составит от
δЗΣмин = 5,8 — 1,06 = 4,74 до δЗΣмакс = 7,28 — 1,06 = 6,22 млн руб. в год, а срок окупаемости капиталовложений — от 21,12 / 6,22 = 3,4 до 21,12 / 4,74 = 4,5 лет.
Результаты расчетов для всех узлов приведены ниже:
Средние значения сроков окупаемости капиталовложений в КУ соответствуют полученным ранее при расчетных реактивных нагрузках. Максимальные значения сроков окупаемости соответствуют ситуации, при которой фактические реактивные нагрузки окажутся меньше расчетных на 10 %, минимальные — обратной ситуации. В первой ситуации мощности КУ окажутся несколько завышенными, в них попадут единицы, которые не окупаются за tок.пр = 5 лет.
Расчет интервалов неопределенности оптимальной мощности КУ
Разложив функцию (7.19) в ряд Тейлора и проведя операции, аналогичные описанным в прил. 4, получим выражение, связывающее абсолютную погрешность производной для /-го узла с погрешностями узловых нагрузок:
Вычислим значения σi для каждого из узлов: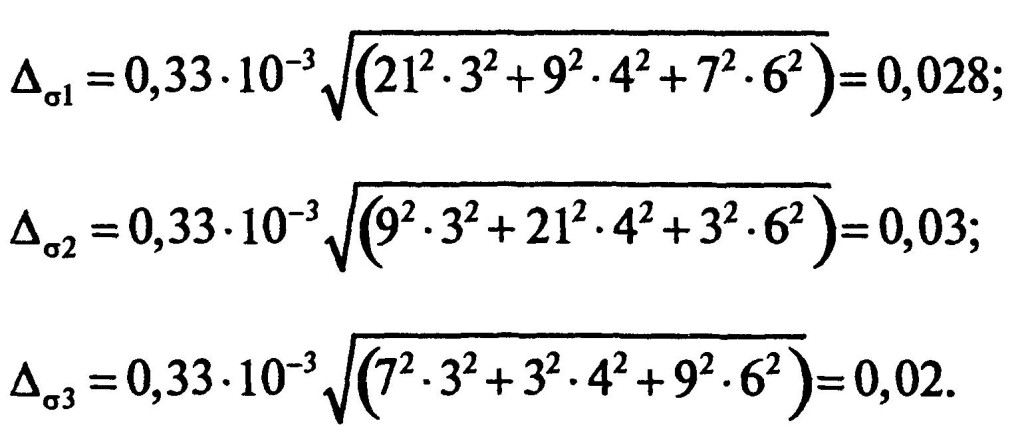
При определении нижних границ интервалов неопределенности оптимальной мощности КУ в узлах необходимо использовать производные (7.21), уменьшенные на Δσi: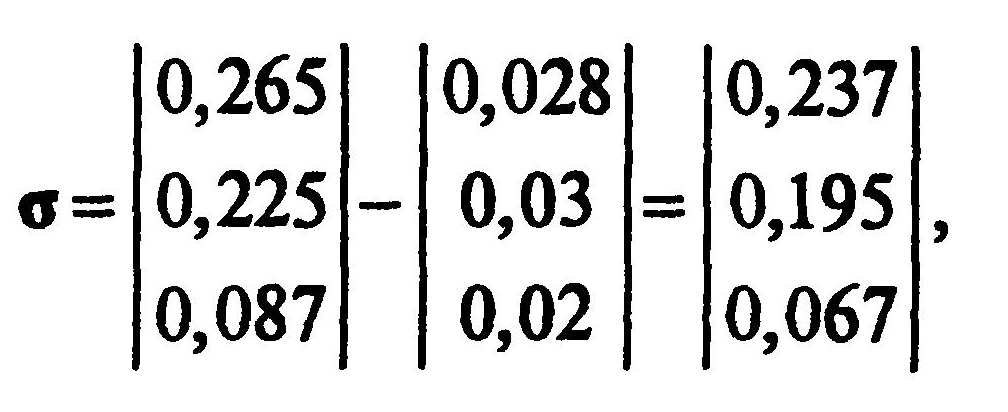
а при определении верхних границ- увеличенные на Δσi:
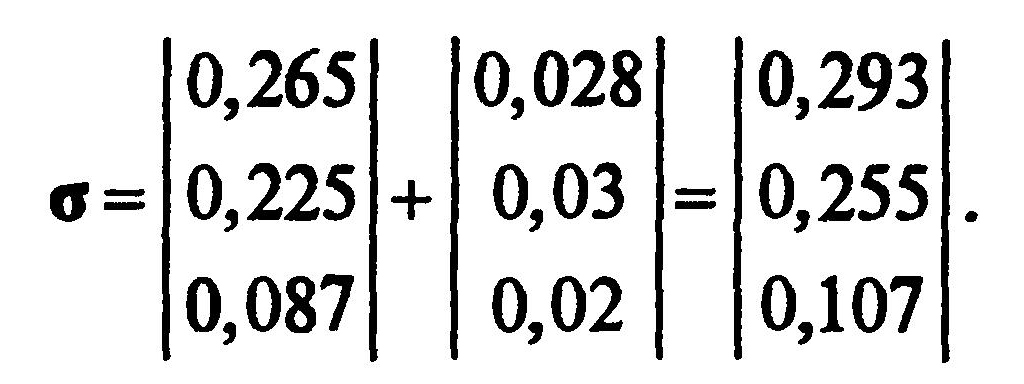Проводя для обоих вариантов матрицы производных итерационные расчеты, аналогичные рассмотренным в п. 7.1.3, получим интервалы неопределенности оптимальной мощности КУ в каждом узле.